0x00 遗传算法 Genetic Algorithm
我们都了解过达尔文的进化论,物竞天择,适者生存,正式这样简单且残酷的自然法则最终在地球上造就了人类这一神奇的物种。我们会制造并使用工具来解决问题,会创作丰富多彩的文艺作品来抒发情感,也能相互合作提高解决问题的效率。而这一切都源于亿万年的时间和无休止的遗传变异、自然选择。
那么如果我们把这样简单的规则应用到计算机程序中,是否同样可以得出一些有意思的结果呢?遗传算法 就描述了这样一种解决问题的思想——仅仅为程序提供随机的初始基因(参数),任其在环境(问题空间)中作出行动(动作空间),并不断选择较为优秀的程序进行繁衍(选取双亲参数组成新程序),淘汰 适应度不佳的程序,加以随机的变异(略微改变子代参数),以求得到适应度最高的种群(收敛)。
遗传算法有许多种具体的实现方法,不同的方法存在一些差异,例如朴素遗传算法中基因为二进制编码的0-1串,在进化策略(Evolution Strategy,简称ES)中基因则为实数向量。本文将主要介绍进化策略的一种最简单实现并给出相应的Python程序示例。
*本文并不会涉及相关理论的数学推导,有兴趣的同学可以自行查阅相关文献
0x01 进化策略 Evolution Strategy
作为一种遗传算法思想的具体实现,进化策略(以下简称ES)主要有如下几个概念:基因DNA,变异率DNA,产生种群,自然选择。
两条DNA
与朴素的遗传算法中定义全局变异率的做法不同,ES在变异率的设置上做了一些优化——除了一条用实数表达的基因DNA以外,额外增加一条与基因等长的、决定对应位置基因变异率的变异率DNA。这条新增的变异率DNA同基因DNA一起参与遗传变异选择,这样做的好处是什么呢?
可以使每个基因位点的变异率随着该基因对适应的贡献程度的增加而趋于0,相当于帮助种群在最优解处收敛。
在本文的实现中,我们的变异率DNA中的数值,将具体定义为对应基因以符合均值为0的正态分布为幅度变异时,该正态分布的标准差$\sigma$。
种群的产生与淘汰
算法开始前,我们完全随机地生成一定数量(Population) 的个体组成初始种群。在接下来的每个事件(Episode) 内,我们根据保留率挑选一部分适应度(Fitness)较高的个体作为下一代的亲本产生下一代,剩余适应度不高的个体被淘汰。经过不断的遗传变异选择,整个种群将逐渐靠近最优解并在其附近趋于收敛。
0x03 代码实现 Talk is Cheap
在本文中我会将代码逐段呈现,想一次性看到全部代码的话请到我的Github。
训练环境
为了简化实验流程并提供可视化的进化过程,我选用了OpenAI Gym作为训练环境。Gym是一个为强化学习研究者编写的基于Python的开源小游戏/环境合集,提供了大量可供使用的训练环境,强化学习研究者仅需关注自己的算法,而不必在测试环境上浪费太多时间。虽然我们的目的是尝试进化策略,但是也可以使用Gym提供的环境。
Gym有几个重要概念,事件(Episode),环境(Environment),观测值(Observation),行动(Action) 以及奖励(Reward) 等,关于这些概念本篇文章不会做过多介绍,近期我会写另一篇文章介绍OpenAI Gym。
在Gym中,每个不同的小游戏可以看作一个环境,在环境中,Agent个体需要根据当前得到的观测值选择下一步的行动(Action),而环境则会在Agent做出行动之后输出四个数据:新的观测值(Observation)、上一步操作中Agent所获得的奖励(Reward)、当前事件(Episode,可以看作是游戏的一局)是否结束(Done)及一些反馈给开发者的信息(Info)。训练的最终目的是得到该环境下一轮事件内能够获得最多奖励的Agent。
下面的代码时Gym的标准使用方式:
1 | import gym |
本文中,我们选取CartPole-v1作为训练环境,在这个环境中,Agent将会学习控制一个能够维持一根木杆平衡的小车。这一环境的观测值包含四个实数(分别表示小车及木杆在上一个动作结束后的某些状态,但是我们不需要知道他们是什么意思),而小车的可选动作(Action Space)只有两种:0、1,分别控制小车向左或向右移动。

编写个体(Agent)
根据ES的基本步骤,每一个个体应该具有两条DNA,能够与其他个体产生子代且能根据外部环境输出相应的行动。由于每次我们可以获得4个观测值,并且只需要控制小车左右移动,我们可以将整个问题看成是一个一次线性函数的拟合(想想为什么),我选择生成包含四个实数的DNA,根据这四个数与观测值对应相乘的和选择小车的两种操作,若大于0则执行操作1,否则执行操作0。
1 | import numpy as np |
进化策略
编写好个体之后,我们就可以开始写进化策略本体了。根据我们之前的描述,程序本体应该包含两个部分:产生种群、自然选择。
我们先来梳理一下ES的整个流程:
- 人为规定种群中个体总数Population以及每次自然选择中要保留的好个体数目Keep
- 产生一个数量为Population的初始种群
- 重复以下过程直到找到最优解:
- 对种群中的每个个体求适应度Fitness
- 根据Fitness从大到小将种群中的个体排序
- 根据Keep保留Fitness排在前面的一部分个体,淘汰其余个体
- 以保留下来的个体作为亲本,产生新的个体填补淘汰出的空位
- 将新的种群投入训练
产生初始种群:
1 | agents = [Agent() for _ in range(population)] |
获取适应度并淘汰落后个体:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30import gym
def get_fittness(agents):
# 在Gym中训练并获得个体适应度
fitness = []
for agent in agents:
agent.fitness = 0
for agent in agents:
observation = env.reset()
for _ in range(50000):
observation, reward, done, info = env.step(agent.calc(observation))
if done:
break
# 根据获得的奖励调整个体适应度
agent.fitness += reward
fitness.append(agent.fitness)
return np.array(fitness)
def choose_agent(agents):
# 获取每个个体的适应度
fitness = get_fittness(agents)
# 将是适应度从大到小排序
fitness_sort = np.argsort(-fitness)
# 选取好的个体加入新种群,淘汰不好的个体
new_agents = []
for i in range(keep):
new_agents.append(agents[fitness_sort[i]])
# 我这里顺便返回了表现最好的个体以供展示
return new_agents, fitness, agents[fitness_sort[0]]
产生新种群:
1 | def make_agent(agents): |
有了这些函数,接下来我们就可以开始进化策略的主程序编写了。
绘制图像
我们希望能有一个直观的方式来展示训练的过程,这里我们可以使用matplotlib来绘制每一代种群中适应度的最大值、最小值和平均值。
我们可以在进化策略的主程序中记录下每代个体的适应度最大、最小和均值,在训练结束后将他们绘制成折线图:
1 | import matplotlib.pyplot as plt |
0x04 训练结果
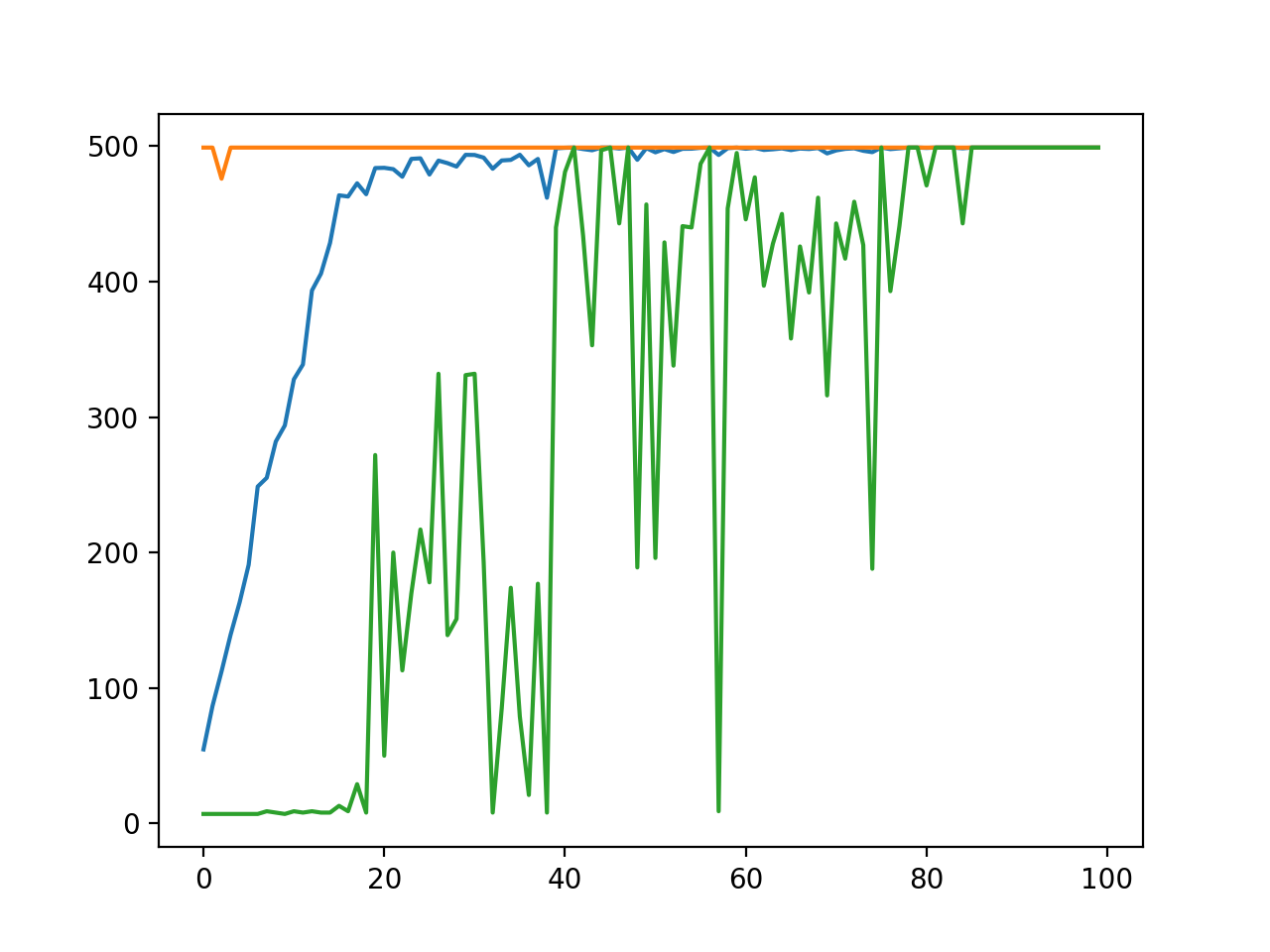
在经过仅仅40代训练后,种群的平均适应度就几乎可以达到满分。