2018-12-16

17 分钟读完 (大约 2517 个字) 0次阅读

数据结构（三）：种一棵圣诞树（上）

0x00 前言

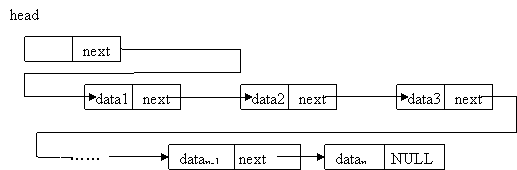
距离上一个教程已经过去一周了，效率很低，很惭愧。不过言归正传，在上一篇文章中，我们着手编写了一个最简单的链式结构——单链表，如果你动手编写了代码，不难发现，教程中采用的编码方式是将数据结构本身抽象成一个结构体（或者面向对象语言中的类），并将每一个最小子节点也抽象成一个结构体。在今后的教程里，我们仍旧遵循这个规则。

在之前的文章中，我们提到了存在一种查询和修改都比较快的数据结构，在这篇文章中，我们会粗略地学到它。不过在接触这种结构之间，让我们先来种下一颗圣诞树。

0x01 什么是树

实际上，如果不实在“数据结构”这个语境下，应该没有人不知道什么是树。回想一下小学一年级的美术课，老师是怎么教我们画一棵树的？首先是画树的枝干，接下来要在树枝根部分叉，在每一条树枝上适当地继续分叉，然后在茂密的树枝边缘画上树叶——实际上树叶还是一种分叉。

在数据结构中，树也差不多就是这么个意思。我们可以把数据结构中的树理解为一个不断嵌套的包含关系：树上的结点可以被别的结点包含，也可以包含其他节点。不包含其他任何结点的点可以称作叶子结点，没有被任何结点包含的点可以称作根结点，其他节点可以称作分支结点或者内部结点。

如果一棵树的结点间有明确的“父节点->子节点”的指向，我们称这种树为有向树，反之，我们称之为无向树。事实上，在使用树结构时，我们一般都是指有向树。最后，我们将以某节点的子节点为根结点的树称作这个节点的子树。

事实上，这种对树的定义是一种不严谨的定义，不过目前为止足够了，在学习完图之后，我们会用图的定义来重新认识树。

在一般的使用中，树常常被用来存储拥有明确的上下级包含关系的数据，比如一个家族的族谱、一个公司的人事信息、门户网站的按类目信息检索、计算机中的文件系统等。这种层级关系可以有效地提升数据查询的速度，通过对数据建立合适的索引，将数据组成一棵树解雇，在可以实现查询过程的每一次决策中只选择一棵子树作为候选结果，这样一来，其他子树可以被直接排除，省去了不必要的遍历，稍后我们会具体讲解这种数据存储方式。

在继续讲解之前，我们现认识一条树的性质——任意一棵有n个结点的树有且只有n-1条边。这其实是树的严谨定义之一，在之后的文章中，我们会加以证明。

0x02 先看东西

树的存储

在这篇文章中，我们依旧采用链式存储结构来保存一棵树。由于上一篇文章已经很详细地介绍了如何编写链式结构，这篇文章中的代码会少一些。

根据管惯例，我们为树本身编写一个结构体Tree，为树的每一个结点编写结构体TreeNode。在设计结构体之前，我们先观察树的结构：一棵树包含很多结构相似的基本结点，每个结点可以拥有一个值，并且拥有任意多个子节点。在上一篇文章中，我们学习了存储任意多数据的方式——链表，所以我们为每个节点创建一个链表来存储它的子节点，在树本身的结构体中，我们只存储它的根结点指针。

最终构建的结构体如下：

typedef /*some type*/ treeElement;
typedef struct Tree  tree;
typedef struct Tree* ptree;
typedef struct TreeNode  tnode;
typedef struct TreeNode* ptnode;
typedef struct List  list;
typedef struct List* plist;
struct Tree {
    ptnode root;
};
struct TreeNode {
    treeElement value;
	plist childList;
};

以上代码省去了链表结构的编写，关于如何编写链表可以参考上一篇文章：数据结构（二）。这种树的存储方式也叫做孩子链表表示法，我们为每一个树结点都创建了一个用来保存它的子节点的链表，实际上，我们还可以进一步简化代码，不创建childList这个链表结构，而是直接存储第一个子节点（孩子链表的头结点），即：

struct TreeNode {
    treeElement value;
	ptnode firstChild;
};

这两种写法本质上没有什么区别，只是维护孩子链表的代码稍有不同，在教程中，为了代码更加清晰，我们采用稍微麻烦一些的第一种写法。

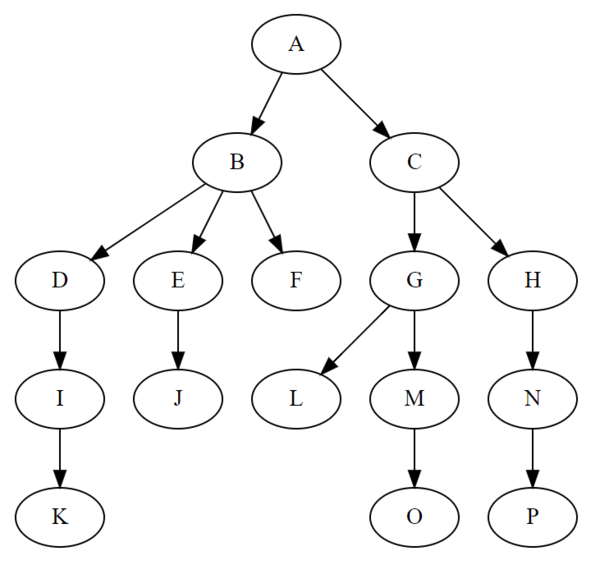
为了举例，我们还是选取上文中的那棵树：

我们随便选取几个结点，看看它们在孩子链表表示法中是什么样的：

结点A

结点A本身的值为A，包含B、C两个子节点，所以这个结点在计算机中的结构如下：

TreeNode A
├── value - "A"
└── childList
    ├── TreeNode B
    └── TreeNode C

结点B

结点B本身的值为B，包含D、E和F三个子节点，所以这个结点在计算机中的结构如下：

TreeNode B
├── value - "B"
└── childList
    ├── TreeNode D
    ├── TreeNode E
    └── TreeNode F

树的遍历

光把数据存起来可不够，我们还需要依照某种顺序把它们不重复不遗漏地读出来，也就是遍历。遍历一棵树有很多种办法，常见的有先序遍历和后序遍历。

先序遍历是指先访问树的根节点，然后再依次先序遍历所有的子树；后序遍历是指先后序遍历子树，然后再访问根节点。这里我们以下面这棵树举例：

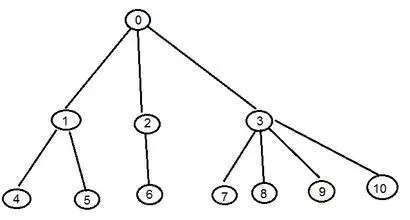
如果对这棵树进行先序遍历，我们将依次访问如下结点：

1	0[1[4, 5], 2[6], 3[7, 8, 9, 10]]

其中方括号表示结点间的包含关系。

如果进行后序遍历，我们将依次访问如下结点：

1	((4, 5)1, (6)2, (7, 8, 9, 10)3)0

其中圆括号表示结点间的包含关系。

具体的代码实现这里暂时不给出了，留做练习以便加深理解。

练习：
编写并完善文章中给出的树的存储结构，将上图的树保村在计算机中，并编写两个函数preOrderTraversal(ptree T)与postOrderTraversal(ptree T)分别实现对树结构的先序与后序遍历，其中传入的参数为树结构体的指针。遍历到一个节点后，只需将它的值打印出来即可。

输入样例：
按照任意方式读入并存储的如下树结构：

输出样例：
先序遍历：0 1 4 5 2 6 3 7 8 9 10
后序遍历：4 5 1 6 2 7 8 9 10 3 0

树的建立

通常在根据已有数据建立一棵树时，我们会给出数据之间的关系，其中一种描述树的方式如下：

第一行为一个整数n，表示树的结点数；
接下来n-1行，每行两个整数x、y，表示x是y的父节点。

按照这种描述方式，上面的树可以表示为如下数据：

在这种情况下，由于总结点数已知，我们建立一个数组来保存每个节点。在一开始，可以先创建n个空的树结点，再建立他们之间的包含关系：

/*------以下代码写在声明区------*/
//由于结点的值就是整数，这里做一个类型别名
typedef int treeElement;
//定义链表类型为树结点，便于使用上篇文章的链表代码
typedef ptnode listElement;
//编写构造空的树结点的函数
ptnode nullTreeNode(treeElement value) {
    ptnode tmp = malloc(sizeof(treeNode));
	tmp->childList = nullList();
}
ptnode treeNodes[11];
/*------以下代码写在main函数内------*/
//读取结点个数
int n;
scanf("%d", &n);
//初始化结点
for (int i = 0; i <= n; i++) {
	treeNodes[i] = nullTreeNode(i)
}

接下来读取数据并做处理：

/*------以下代码写在声明区------*/
//编写函数用于将两个结点连接起来
void connect(ptnode father, ptnode child) {
    
}
/*------以下代码写在main函数内------*/
//读取结点关系
for (int i = 0; i <= n-1; i++) {
    int x, y;
    scanf("%d %d", &x, &y);
    //这里的addToList函数在上篇文章中没有写出，请试着自己完成，作用是将一个值插入到链表尾部
    addToList(treeNode[x]->childList, treeNode[y]);
}
//以0号结点为根结点构建一棵树
ptree tree = newTree(treeNode[0]);

这样就完成了树的构建。构建树还有很多方式，我们在之后可能会讲到。

这一篇比我预想的要长太多了，暂时先在这里截断吧，用这些知识可以完成本篇文章的练习题，请先完成它。

# 教程, 数据结构