0x00 前言
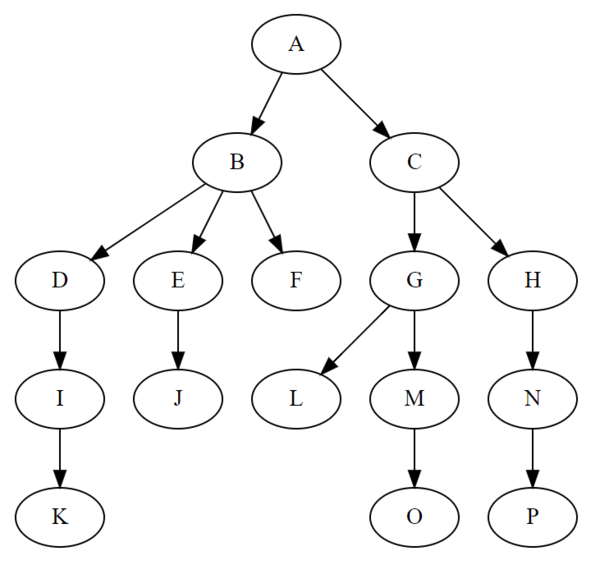
什么是数据结构?
提到数据,我们应该并不陌生。生活中我们每天都要接触各式各样的数据——支付宝还有多少余额、花呗白条要还多少钱、饭卡电话卡这个那个卡是不是该充值了……但是提起数据结构,就显得抽象了许多。
如果仔细思考就能发现,我们生活中的数据并不是独立存在彼此互不关联的。恰恰相反,我们平时见到的数据往往通过各种关系密切地联系起来,形成一个个的数据集合:一个班内所有学生的信息一同组成班级学生信息,银行卡微信支付宝余额一同组成我们的个人财富、想要知道某位老师的邮箱得从学校主页到学院主页再到教室信息页面……事实上,我们可以把数据和数据之间的全部关联组成的集合称作一个数据结构。在离散数学中,常常用序偶(二元组)的形式来描述数据之间的关系,称一些而元组的集合为关系。事实上,如果不考虑数据结构的具体数据,则其结构本身就可以看作一个关系。
0x01 数据存储
根据上面的定义,数据结构可以拆分为两个部分,数据与结构。其中,结构是抽象的数学概念,而数据则由结构组织起来。实际上,当我我们谈论某种数据结构时,往往讨论的是其结构部分,而不关心数据内容。但是当我们使用或者保存一个数据结构实体的时候,就要关注这些数据本身了。
那么如何把这些由抽象的数学关系组织起来的数据保存到我们的计算机中呢?我们首先要了解内存是什么样的。
内存
我们不必关心计算机内存究竟是如何工作的,事实上,我们只要了解内存的数据存储结构就可以了。用一句话来描述,内存可以通过一串地址信息来获取存储在这个地址上的数据。那么什么是地址呢?
假设有一条长长的街道,这条奇怪的街道上每隔一定距离就会有一个房屋,这些房屋的门牌号从0开始编号,每户增加1。有意思的事,这些房屋平时并不住人,只有在街道办的安排下,住客才能临时占有一间屋子。即便这样,这些住客也不是就在这里住下不走了,只要街道办有要求,他们就得根据要求换到指定门牌号的另外一间屋子去,甚至有时候还会被街道办赶出这条街道。
计算机的内存就是这样一条街道,只不过房屋里面住的不是住客,而是数据。相应地,这些房屋的门牌号就被叫做内存地址。只要你向街道办提供内存地址信息,街道办的小喽啰就可以马上把那间屋子里的数据抓来给你看。
正是因为内存结构的特殊性,我们只能把数据排成排存进去,就算你的数据之间有着明确的层级关系,我们也没有办法在内存中直接表示出这种关系。这样一来,就有必要认真考虑考虑究竟该怎么样往内存中存数据了。
存储结构
上面已经解释了内存的特殊结构,接下来我们针对不同的数据分门别类地想一想怎么把它们合理地放进内存。
以我们最最常见的一组数据——某个地铁的线路为例,我们有两种存储方式。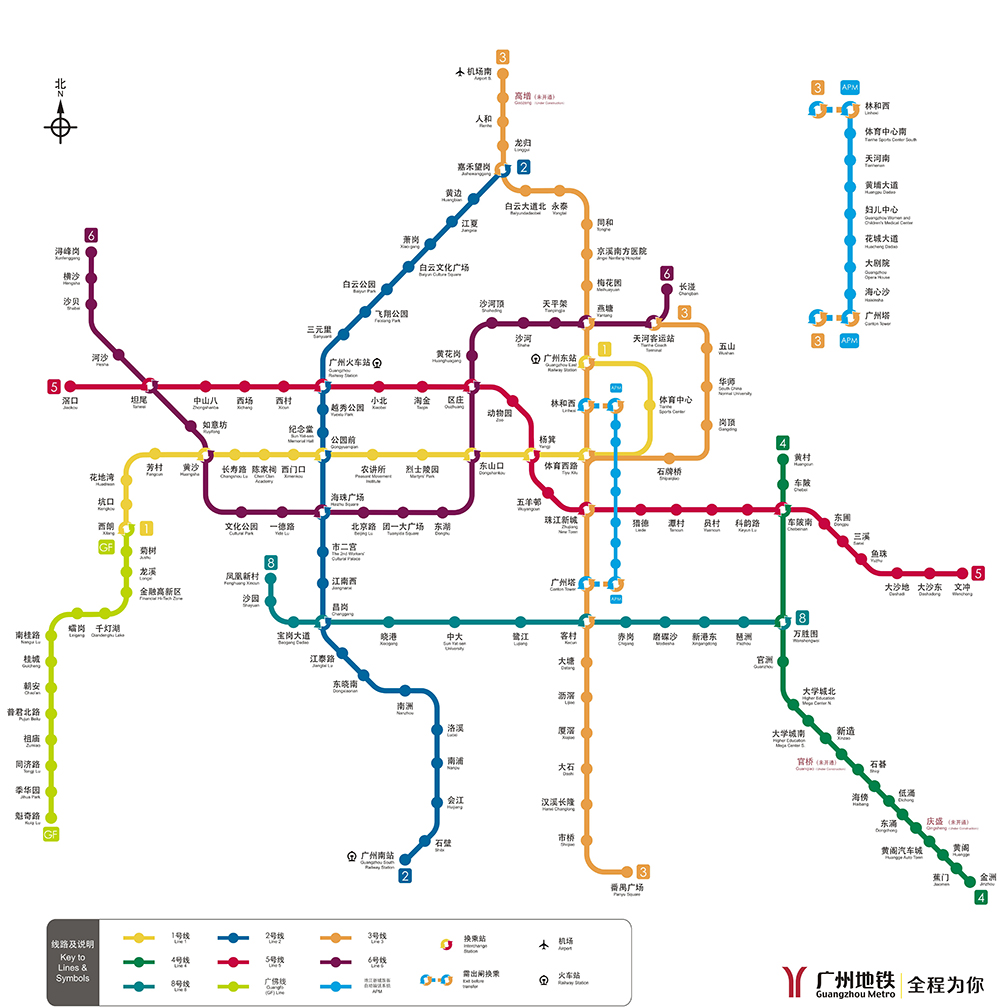
上面是某个城市的地铁线路图,我们只看其中的某一条线。不难发现,地铁的途径站点一个接一个地排在一起,组成长长的一串——这下正好,我们的内存也是一个长条形状的,那能不能直接把这些数据一个接一个紧挨着放到内存里呢?当然可以,事实上这就是第一种数据存储结构——“顺序存储结构”。
在顺序存储结构中,一组数据要占据一段连续的内存地址,这就要求我们预先在内存中找到一段足够放下这些数据的空间——要足够长,中间也不能有别的数据。这就是C语言中malloc的含义,预先分配一个指定大小的内存区间。这种存储结构有一个极端显著的优点——方便。这里的方便可不仅仅是指存放数据时简简单单一个挨一个放的方便,更重要的是这种结构存储的数据特别容易查询。比如我们在内存的第31号地址和第40号地址之间存了一个地铁的途径站点,那当我想知道这趟地铁第3站是哪一站的时候,直接去找内存的33号地址上的数据就可以了。但同时,这种结构也存在一个显著的缺点——不方便修改。如果这趟地铁突然维修,在某两站之间加了一站,这可就坏事了,我们得吧内存中增加了的那站之后的所有站点全都挨个儿往后移动一位,这样一来,费时费力不说,还有可能害得最后几个数据无家可归——如果这一串内存空间的后面恰巧有了别的数据,那移动后的数据很可能和那些原有的数据相互冲突。就比如我们的数据存在内存的第31号地址和第40号地址之间,但是第41号地址上恰巧已经有了一个其他的数据,这个时候我们把新增的站点插进来,就会导致原来在40号地址上的数据没地方放。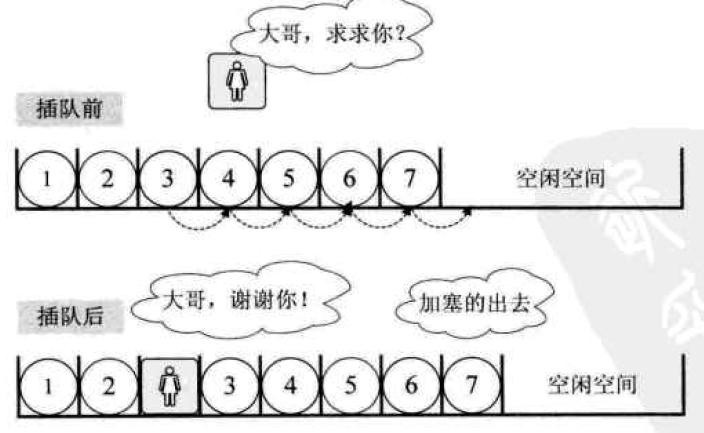
你可能会说了,放到第42号地址不行吗?还真的不行。我们之前说,这段数据一定要在内存中连在一起,这样才能快速地找到特定位置上的数据,一旦这些数据不连着,没办法直接找到特定序号的数据不说,我们连那些地址存着的是我们的地铁线路信息都搞不清楚了。
既然这种顺序存储这么麻烦,那有没有一个能解决这个问题的存储方式呢?毕竟谁也不能保证自己常座的地铁永远也不会改线路是不是。
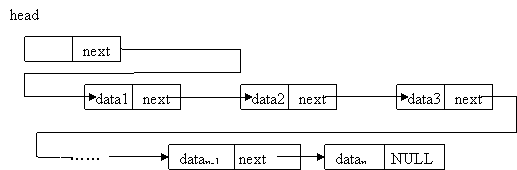
你应该还记得赏金猎人的游戏规则,玩家一开始先拿到一个谜题,谜题的答案是下一条谜题存放位置的线索,玩家顺着一条条线索摸索下去,最终就能解开所有的谜题获得胜利。这么一看,好像这些谜题也像地铁站点一样有着一定的先后顺序,可是这些谜题也没有按照前后顺序摆放呀?事实上,这种一个谜题提示你下一个谜题存放位置的存放方式正是内存中数据存放的第二种办法,“链式存储结构”。
这种存储结构的核心思想是,数据不依照实际的顺序或者关系保存在内存中,而是随便想放在什么地址就放在什么地址,但是存放的每一个数据都一定要同时包含每个和自己有关联的数据的存放位置。就拿地铁线路举例,我们可以随便把站点名字存在什么地址上,但是一定要在这个地址旁边再存一个数据,这个数据用来表示下一站的站点名字在内存中的地址。这样一来,我们只要记住始发站的内存地址,就可以每次读区旁边的那个数据来找到下一站的地址了。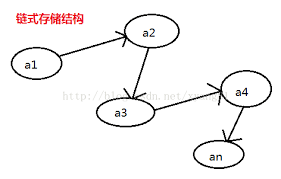
说了半天,这种结构到底有什么优势呢?首先可以想到的是,存储数据再也不需要找一段连续的内存单元了,这样一来,也自然不必担心新增数据的时候没地方放的问题。更有趣的是,向链式存储的数据中添加数据也没有顺序存储的数据那么麻烦了,比如我们想在A和B两站中间修一个C站点,那么只需要先在内存里找一个空位把C的名字存起来,在它旁边存储下一站(也就是B站点)的内存地址,然后把A站点旁边存储A的下一站内存地址的数据修改为C的内存地址,简单三步就完成了新站点的添加,还不用担心把什么数据搞的无家可归,多么美妙。
当然了,常识告诉我们这个世界上没有绝对完美的东西(谁知道呢),链式存储结构也有一个不方便的地方,如果我们想知道第10站是哪一站,就必须从第一站开始,一次又一次地找下一站的地址,然后去那个地址继续找下一站的地址,直到找到第10站,远比顺序存储时直接访问(第一站地址+10)这个地址要麻烦的多。
这两种存储结构各有利弊,有没有什么完美无缺的存储方式呢?当然——
想什么呢,怎么可能,要是有的话还学什么数据结构。
不过话说回来,到时的确有一些基于这两种最基本的存储结构而衍生出来的数据结构,可以实现较快的查找和较快地修改,不过这些内容都是后话了,这篇文章暂时就到这里。
0x02 下集预告
在下一篇文章中,我们会学到一种最最基本的数据结构——链表以及它的创建方式,还会掌握一些实际编码中的小技巧。